qc7大手法之直方图

关键词：qc7大手法,直方图

作为qc7大手法之一的直方图，其作用是说明观测范围内数据出现的频率，表明数据的分布与规格的联系以及数据是否超出规格限制范围。我们透过直方图的形状，数据的中心值，数据的离散方式可以知道一个过程的许多信息，从而判断过程的品质。

建立qc7大手法直方图的步骤：

1. 收集和记录数据。许多信息依赖于所收集数据的类型和记录的方式。

2. 确定数据的最大值和最小值。查找数据的最大，最小值。

3. 决定分组的数目。经验告诉我们，通常使分组的数目与观测数据量的平方根大致相等。

4. 确定每组数据的极差。每组数据的极差必须相等，如果观测值是舍入值，这将使问题易于处理。让极差的起始值和终止值落在两个数值之间，这样就能很容易看出数据所在的范围。

5. 设定各组的宽度。宽度可由（最大值－最小值）除以分组数得到。

6. 画一表格来记录数据。表格里的每行反映直方图的范围。

7. 记录数据，检查每个数据，并在相应的行做标记。接着，合计每行的标记数，如下所示。

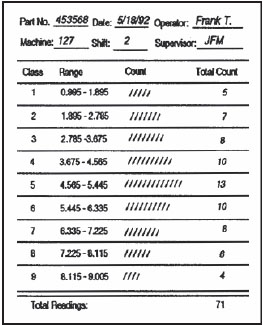
qc7大手法——记录直方图数据

8. 建立平面坐标系。两坐标轴应足够长，能包含所有的数据点。可能还需在直方图里标出生产指标线，上限和下限。

9. 作直方图。根据步骤 5决定柱体的宽度，高度应等于表格中记录的频数。图A给出了上述数据的直方图。

 
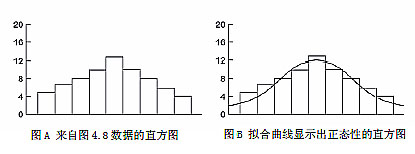
qc7大手法——直方图

怎样解释图表取决于你的目的和数据的分布。近似正态分布的形状意味着过程的变化源于普通原因。如图 B所示，正态分布是对称的。

实际分布与正态分布曲线的接近程度能告诉我们过程的许多信息。虽然我们通常能看到分布是否接近正态，但我们并不能每次都识别出反映过程问题的微小变化，在qc7大手法中，直方图尤其是这样。

在qc7大手法中，直方图是使用频率最高的图表之一，因为我们可以通过直方图直观地观察到数据的分布趋势以及是否超过公差限范围，从而判断生产过程能力是否足够，为保证稳定的生产过程提供可靠依据。