qc7大手法散点图的定义、分类与应用范围

关键词：qc7大手法,散点图

散点图又称散布图，是指通过分析研究两种因素的数据之间的关系，来控制影响产品质量的相关因素的qc7大手法之一。

qc7大手法——散点图的目的

• 研究两变量之间是否存在关系；
• 研究一对连续变量之间的潜在关系；
• 用一变量变化说明另外一变量变化状况；
• 改变一个变量，对另外一变量施加影响。

qc7大手法散点图的定义、分类与应用范围

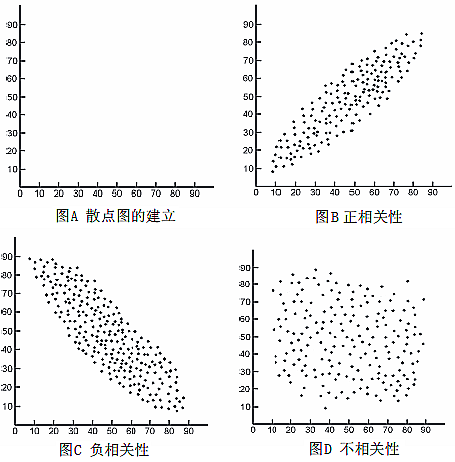
qc7大手法——散点图分类

• 强正相关。x增大，y也随之线性增大。x与y之间可用直线y=a+bx(b为正数)表示。此时，只要控制住x，y也随之被控制住了。
• 弱正相关。点分布在一条直线附件，且x增大，y基本上随之线性增大，此时除了因素x外可能还有其他因素影响y。
• 无关。X和y两变量之间没有任何一种明确的趋势关系。说明两因素互不相关。
• 弱负相关。X增大，y基本上随之线性减小。此时除了x之外，可能还有其他因素影响y。
• 强负相关。X与y之间可用直线y=a+bx (b为负数)表示。y随x的增大而减小。此时，可以通过控制x来控制y的变化。
• 非线性相关。X、y之间可用曲线方程进行拟合，根据两变量之间的曲线关系，可以利用x的控制调整实现对y的控制。

qc7大手法——散点图应用范围

• 能大概掌握原因与结果之间是否有关联及关联的程度如何。
• 能检查离岛现象是否存在。
• 原因与结果关联性高时，二者可互为替代变数。对于过程参数或品特性的掌握，可从原因或结果中选择一较经济性的变数予以监测。
• 可通过观察一变数的变化来知道另一变数的变化。
• 当不知道两个因素之间的关系或两个因素之间 关系在认识上比较模糊而需要对这两个因素之间的关系进行调查和确认时，可以通过散点图来确认。

qc7大手法——散点图应用注意事项

• 要注意对数据进行正确的分层，否则将会导致不真实的判断结论。
• 散点图中出现的个别偏离分布趋势的异常点，应在查明原因后予以剔除。
• 散点图相关性规律的适用范围一般局限于观测值数据的范围内，不能任意扩大相关判断范围。
• 当收集到的数据较多时，难免出现重复数据。在作图时，可用双重圈表示，或者在点的右上方注明重复次数。
• 又相关分析所得出的结论，应注意数据的取值范围。一般不能任意更改其适用范围，当取值范围不同时，应再做相应的试验与分析。