质量管理中的正态分布

关键词：正态分布,质量管理

正态分布是在质量管理中最重要最常使用的分布，它能描述很多质量特性X随机取值的统计规律性。

正态分布的概率密度函数有如下形式：

它的图形是对称的钟形曲线，称为正态曲线，见图一。

图一，正态曲线，μ为正态分布中心，μ±σ为拐点

正态分布含有两个参数μ与σ，常记为N（μ，σ2）。其中μ为正态分布的均值，它是正态分布的中心，质量特性X在μ附近取值的机会更大，P(x)关于x=μ对称。σ2是正态分布的方差，σ＞0是正态分布的标准差，σ愈大，分布愈分散；σ愈小，分布愈集中；P(x)在μ±σ处有拐点（2阶倒数为零）。 固定标准差σ时，不同的均值，如μ1＜μ2，对应的正态曲线的形状完全相同，仅位置不同，见图二。

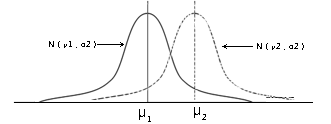
图二，σ相同，μ不相同（μ1＜μ2）

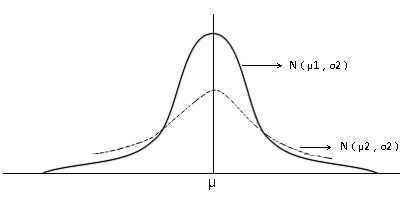
固定均值μ时，不同的标准差，如σ1＜σ2，对应的正态曲线的位置相同，但形状（高低与胖瘦）不同，见图三。

图三，μ相同，σ不相同（σ1＜σ2）

以上介绍了正态分布的计算公式、标准曲线图、标准差均值分别固定的两种曲线图。正态分布与质量管理紧密相连，我们所熟知的SPC控制图就是由标准正态分布曲线图旋转90度得来。因此，学好正态分布有利于深入理解质量管理并开展工作。想要了解更多正态分布知识，请关注英国威廉希尔体育公司官网SPC知识库。