直方图应用步骤及分析详解

关键词：直方图，直方图的作用，直方图分析

直方图（histogram）

直方图是从总体中随机抽取样本，将从样本数据加以整理，用于了解数据的分布情况，使我们比较容易直接看到数据的位置状况、离散程度和分布形状的一种常用工具。它是用一系列宽度相等、高度不等的长方形来表示数据，其宽度代表组距，高度代表指定组距内的数据数（频数）。（直方图适用于连续性数据） 

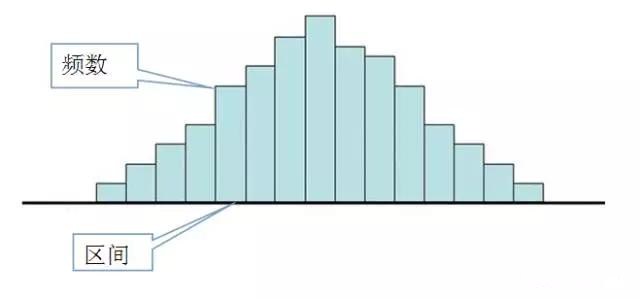
我们要如何解读直方图？第一步应先大致了解一下直方图有哪些作用：

直方图的作用

直观地显示质量特性的分布状态，对于数据的分布的形状、中心位置和分散程度一目了然；

关注数据和规格的关系，通过测定值与规格值比较，判断出不良是平均不良还是异常的不良，便于人们确定在何处进行质量改进；

（在此对平均不良和异常不良作个解释：平均不良通常代表的是系统的问题，是整个过程的不良；异常不良却代表了个别的离散的不良，属于个别问题。）

比较改善前后的直方图，可了解平均值、分散、分布形状的变化，改善的效果如何。

解读直方图

首先我们要了解直方图的形状，通过直方图的形状了解过程是否异常。

一．直方图的形状：

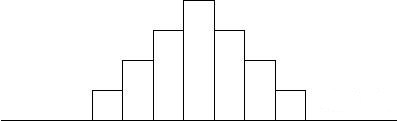
1.常态型：中间高、两边低、有集中边势，显示过程正常。

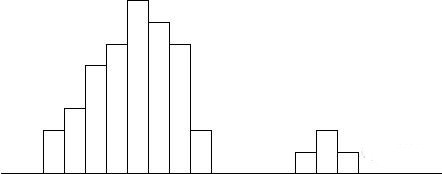
2. 离岛型：在右端或左端形成小岛。说明一定有异常原因存在，如数据收集方法错误、数据来源不同或新手作业违背操作规程等特殊原因，需迅速追寻原因，采取必要措拖。

3. 双峰型：有两个高峰出现。两台不同的机器或两种不同原料间存在差异时，或者作业者不同时也可发生此类直方图。例如，病历质控的2位质控员对检查标准掌握有差异时，又或者同一位质控员应用两种评估标准检测的结果。出现这类情况时，应将数据层别处理后再制作直方图。

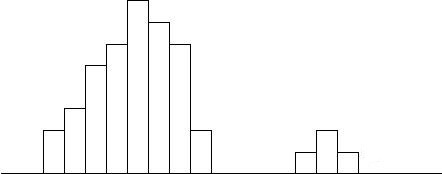
4. 锯齿型：图形的柱形高低不一，呈现缺齿的形状。这种情况大多因为制作直方图的方法错误（如：数据分组问题、计算组距问题、计算界限问题等）或数据收集方法不正确（如：不同设备数据、不同人收集的数据、不同时段数据造成）产生。

5.偏态形：高处偏向一边,另一边低,拖长尾巴。可分偏右型,偏左型。这种偏态分布理论上是规格值无法取得某一数值以下所致，在质量特性上并没有问题，但我们需要留意拖长的尾端在技术上是否可接受，同时应考量制程能力，如过程能力不够时需进行改善。

6.高原形：直方图的柱子高低近似，柱子间高度相差甚微，看起来有点像高原一样，则称为高原形。当数据来自几种平均值差异不大的产品，而这些产品有混在一起时，制作出来的直方图往往就是高原形，应层别之后再作直方图比较。

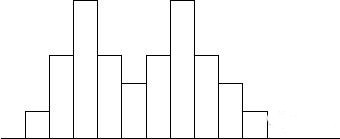
二．与规格比较：过程是否异常除了查看直方图的形状，还要结合产品的规格一起来评估。

在这里先解释一下什么是规格，规格通常是根据客户要求来定的（产品的规格），然后在实际工作中，收集数据计算出控制限。如果客户没有给出，就以行业标准为准。

规格又分为双侧规格（同时有上下限的要求）和单侧规格（只有上限或下限的要求，如时间数据、分值数据等）

直方图与规格比较时又分为符合规格和不符合规格两类：

（一）符合规格：

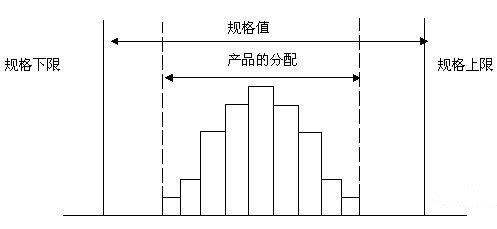
1.理想型：规格值的平均值与产品的分布平均值重合，而且直方图的下限与上限均在规格值的上下限范围之内，直方图的下限与规格值的下限、直方图的上限与规格值的上限之间的距离为4个标准差左右，这样的直方图时最理想的直方图。

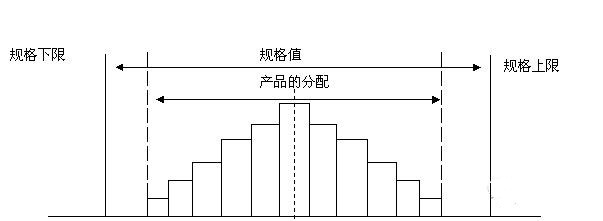
2.一侧无余裕：产品的分布均在规格值范围内，但是偏向上限或者下限分布，造成单侧拥塞，另一边余裕很多。若过程再变大(或变小)很可能会有不良发生, 必需设法使制品中心值与规格中心值吻合。

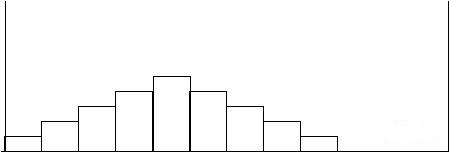
3.两侧无余裕：产品分布的下限与规格下限重合，分布上界限与规格上限重合，即分布与规格恰好相等。虽没有不良发生，但过程稍有变动，就有不良品发生的风险。最好是平均值保持原状，但变异方面采取缩小的对策。

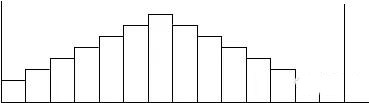
4.余裕太多：也就是过度集中，该类产品分布的范围较小，而规格值的范围太大，也就是说制程的能力远远大于规格的要求。看上去非常好的图型，但如果此种情形是因增加成本而得到, 并非好的现象, 故可考虑缩小规格界限或放松质量变异, 以降低成本、减少浪费。

（二）不符合规格：

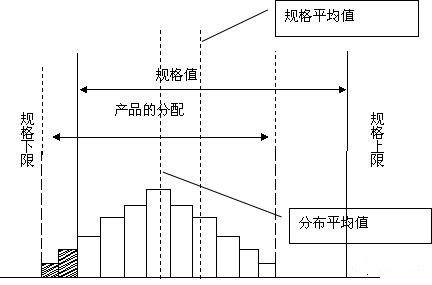
1.平均值偏左（或偏右）：也叫单边不良形，表示平均位置有偏差，应考虑过程的能力不足，需寻找系统原因，纠正平均值位置，提高品质水平。

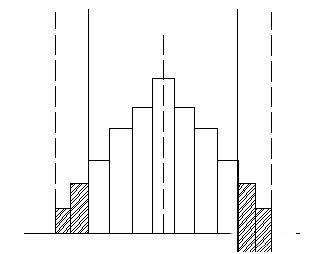
2. 分散度过大：也可称为双边不良形。产品的最大值与最小值均超过规格值, 有不良品发生表示标准太大, 制程能力不足。应针对变动的人员、方法等方向去追查, 要设法使产品的变异缩小; 如果是规格订得太严, 应放宽规格。

3.离岛现象：有“离岛”产品出现，且发生不良现象，说明过程有异常原因存在，应调查离岛的原因，判明离群原因（通常为特异原因）并予以去除。

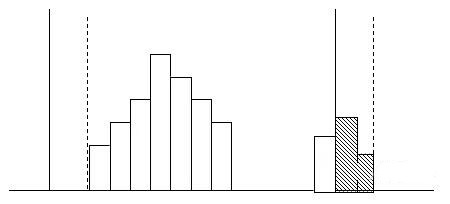
直方图的制作

制作直方图的步骤：

第1步：整理数据表，用随机抽样的方法抽取数据，一般要求数据在50个以上。

【例】某医院门诊部对内科病人候诊时间进行抽样调查，测量了2月份60位病人的等候时间，经整理如表1

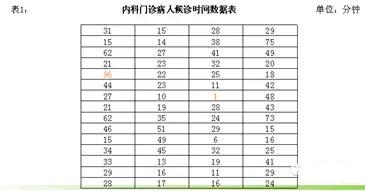
第2步：计算全距（R）：也叫极差，是所有数据中最大值与最小值的差。

R=Xmax - Xmin =96 - 1 = 95

第3步：确定组数（k）。组数不可过多过少，过少，会掩盖数据的分布规律；组数过多，使数据过于零乱分散，也不能显示出质量分布状况。组数的确定可有两种方法：

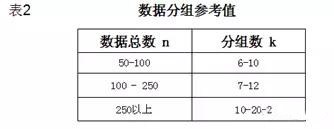
方法1：可参考表2的经验数值

方法2：很多情况下，分组数约等于样本容量的平方根是比较合适的：表1中有60个数据点，应分组数为：k = √60 ≈8

第4步：决定组距（d）。组距是组与组之间的间隔，也即一个组的范围。因为各组距应相等，于是有：

组距（d）= 全距（R）÷组数（k）= 95÷8=11.875≈12

（为便于计算平均数与标准差,组距常取为5的倍数或10的倍数,或2的倍数）

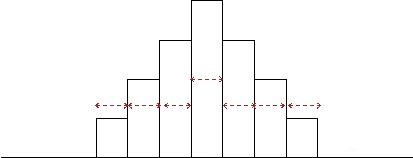
第5步：决定各组的上下组界。每组的最大值为上限，最小值为下限，上、下限统称组限

最小一组的上组界=下组界（最小值－测定值最小位数/2）+组距 = 0.5+12 =12.5

……

依此类推,计算至最大一组之组界

第6步：制作频率表

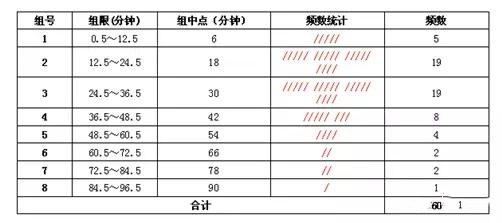
第7步：画直方图（简单直方图）

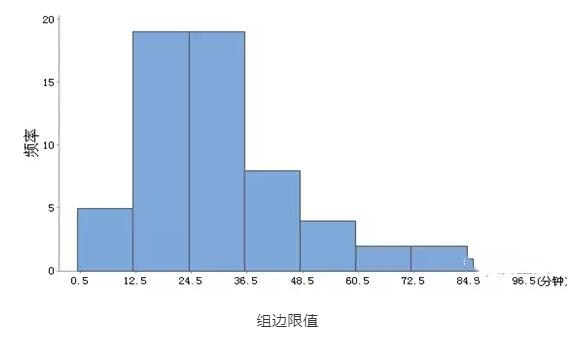
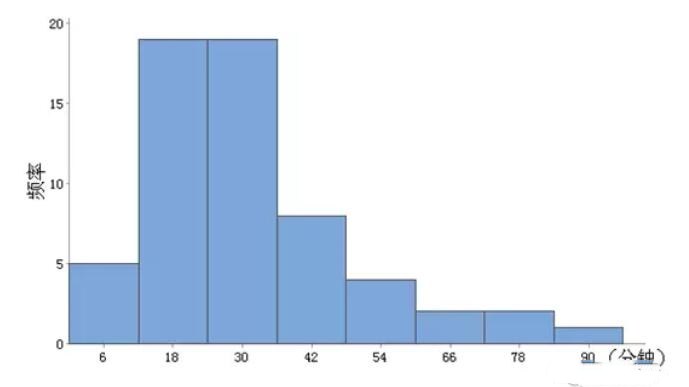
以横坐标表示各组的中点或组限，纵坐标表示频数，画出直方图

组边限值

组中值

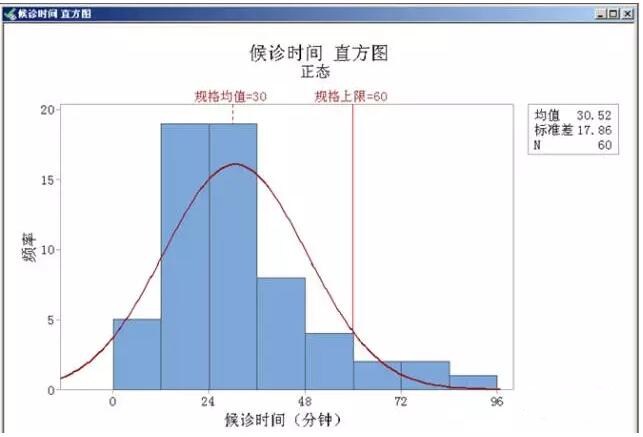
第8步：加入必要的元素：样本大小、均值、标准差、规格均值、规格上下限

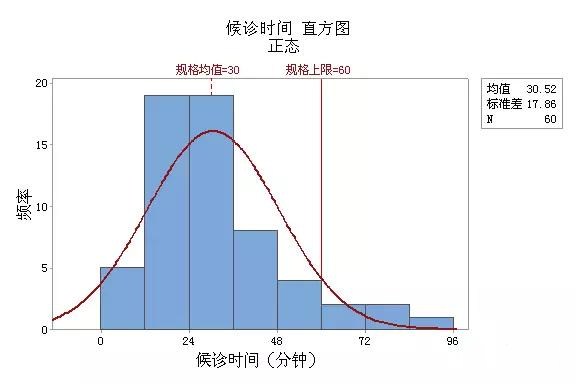
注：此图因为时间数据，只有上限要求，因此只有一条规格线

解释结果：

样本均值为 30.52，略高于目标值30，但已经很接近了。分布呈右偏斜，说明尚有部份候诊时间偏长，且有5例候诊时间过长，超过规格上限60分钟。对此我们可针对超出规格上限的不良事件找寻原因，纠正缺陷，去除不良影响，以改善整体的分布形态，提高过程能力。

软件绘制直方图步骤

目前我们可用来绘制直方图的软件有EXCEL和MINITAB。由于使用EXCEL制作直方图过程较复杂，需占用较多时间去完成。而MINITAB软件在制图方面，操作简单，容易掌握，花费时间少。因此，这里只介绍使用MINITAB软件制作直方图的过程。

第1步：打开MINITAB软件，在新建工作表里导入一组数据（可从EXCEL表中复制数据，粘贴到工作表中）。

第2步：菜单栏中选择“图形”，在图形下拉栏点“直方图”

第3步：点击“直方图”后将跳出下面的对话框，因我们只需绘制简单的直方图，所以选择“简单”图形，点“确定”键。

第4步：进入下面的对话框时，将鼠标移至左边方框内双击选择“候诊时间”，此时“候诊时间”的数据列已选中进入“图形变量”框内。

第5步：点“确定”键进入下一步，直方图的初型已完成。

在此需要强调一下，因为软件设定的分组规则与人工计算的方法不一样，经过反复验证发现MINITAB的分组规则是样本容量在100以下均为11组，样本容量大于100的分组是20组。所以根据实际情况，我们可区间的参数进行调整。

第6步：调查区间数。

⑴ 单击柱状区域，令每个柱子的边角位出现白色小方格

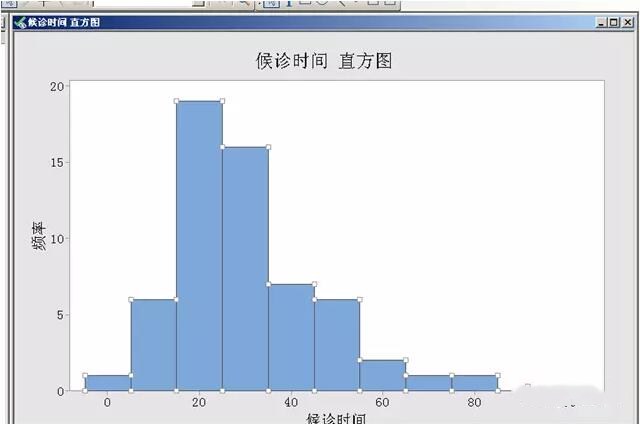
⑵ 鼠标点右键在出现的菜单框内选择“编辑条形”，便出现以下对话框：

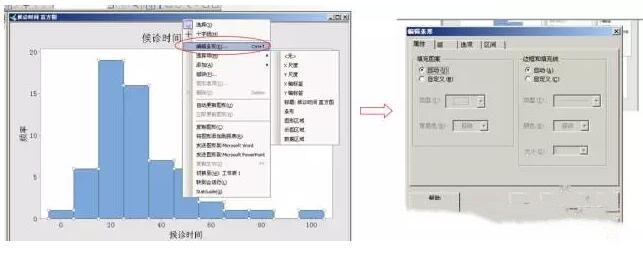
⑶ 点击“区间”可见：这里可以看到区间数为11，下一步我们要将区间数改为8。

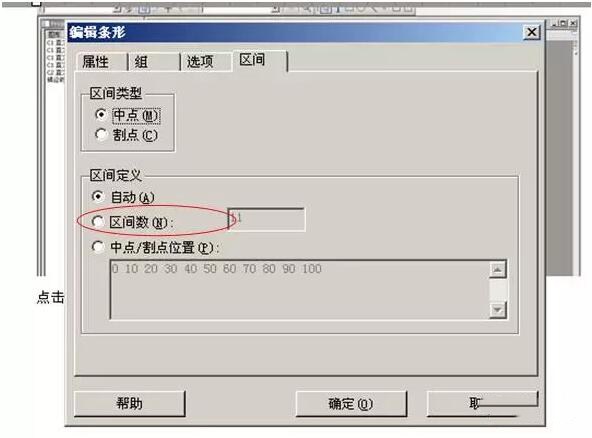
⑷ 点中“区间数”前面的选项框，“区间数”右边的数字框底色变白，里面的数字可调整。将11改为8，按“确认”键。

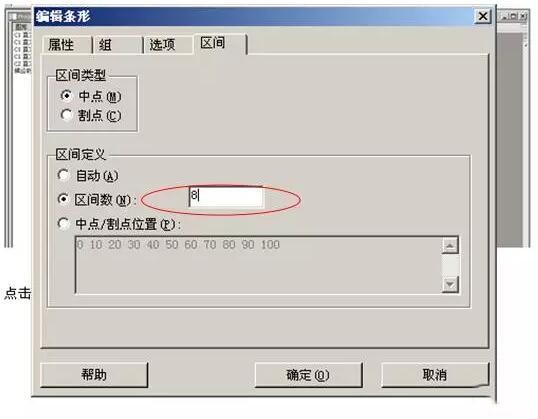
⑸ 已成功改为8组区间的直方图：

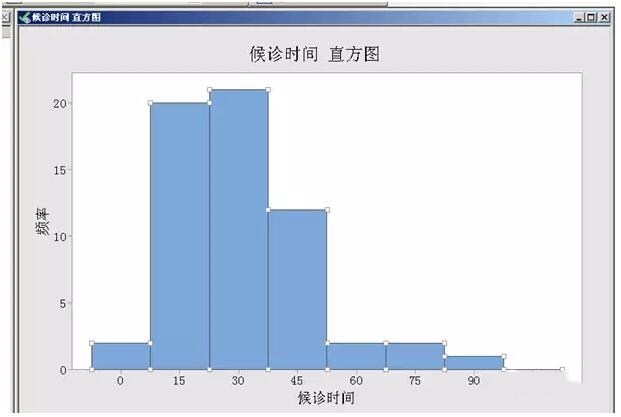
因为我们取的是时间数据，不会存在0以下的数值，我们看到软件直动生成的组中值是0，区间下限是-7.5，所以接下来我们还要对区间的上下限设定进行修改。

第7步：调整组限。

⑴ 重复第6步的（1）—（3），进入以下界面：

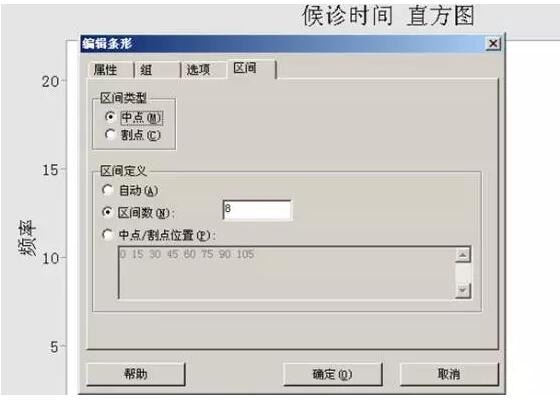
⑵ 将区间类型的“中点”改为“割点”，确定后可见下图。如果有需要我们还可对“中点/割点位置”内的数值进行修改。

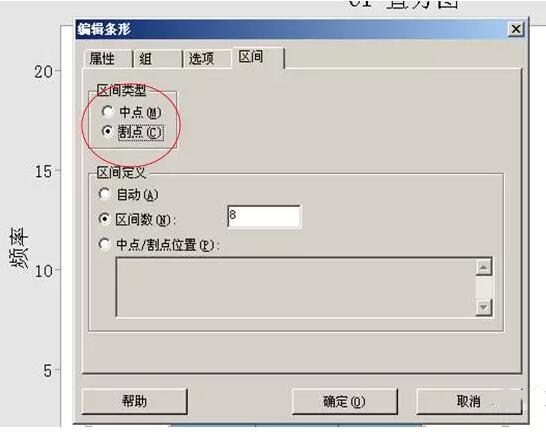
⑶ 已成功修改了组限的直方图：

第8步：在图形中加样本数、均值、标准差

⑴ 将鼠标移至图形中央，点右键，在菜单框内选择“添加”→“分布拟合值”

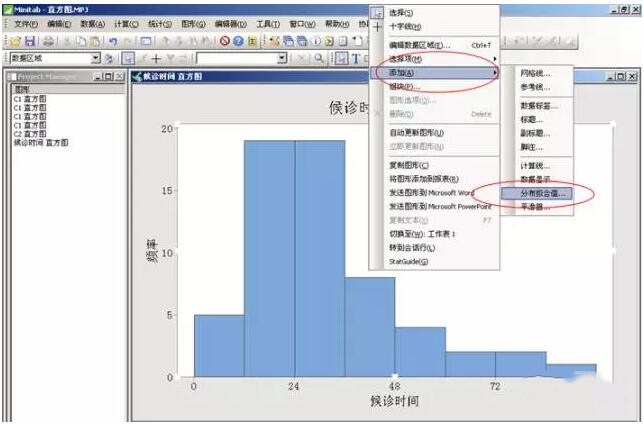
⑵ 在下面的对话框中选“确定”

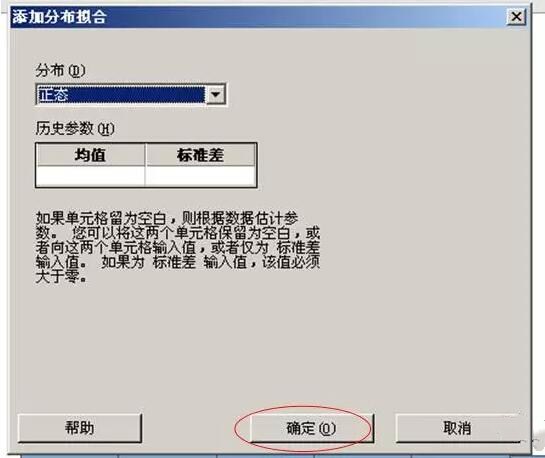
⑶ 图形中增加一条正态分布的概率密度曲线，右侧标有样本数、均值和标准差。

第9步：插入规格均值和规格上下限

⑴ 将鼠标移至图形中央，点右键，在菜单框内选择“添加”→“参考线”

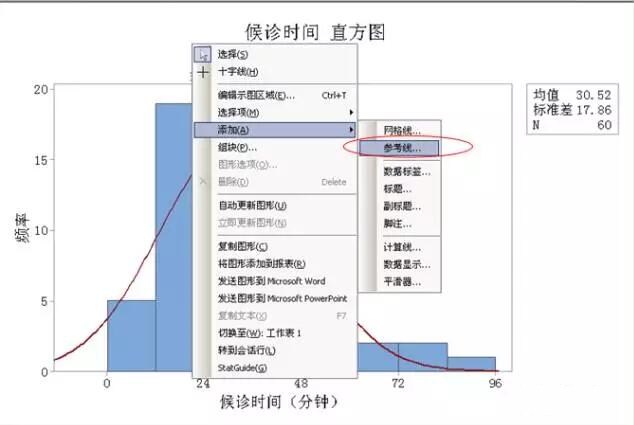
⑵ 规格均值线和上下限线是由X轴插入，所以要将光标移到“在数据值处显示参考线”。

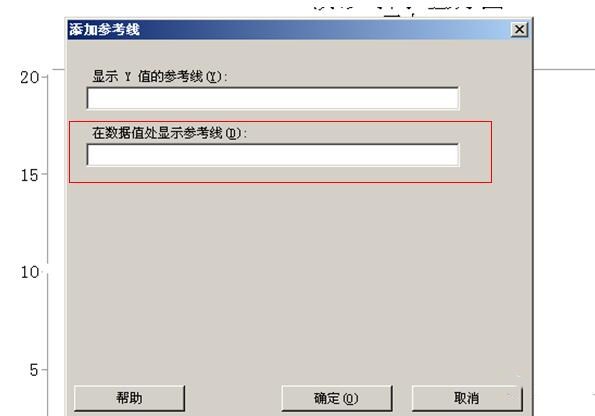
⑶ 如果要设定的目标平均值是30分钟，目标上限是不超过60分钟，就在“在数据值处显示参考线”下端的框内键入数值“30”确定后再重复第9步的⑴重新进入上面的对话框，再次在“在数据值处显示参考线”下端的框内键入数值“60”，便可得到下图：

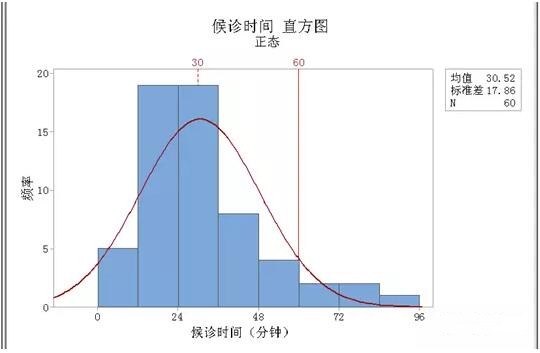
⑷ 为了清晰定义插入的两条参考线，还需对“30”和“60”的数值标签进行编辑。选中数值“30”，点右键，选“编辑X线条标签”。

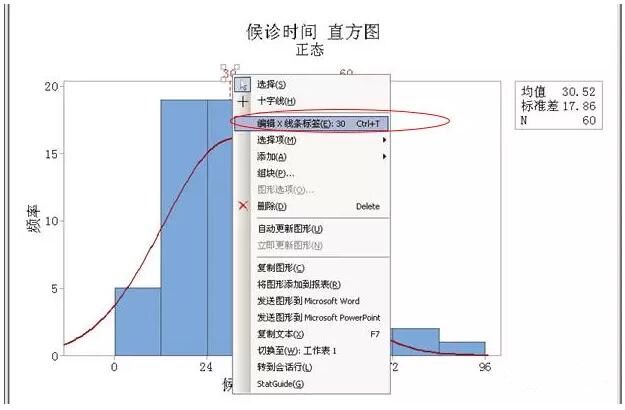
⑸ 在“文本（T）”下框中键入“规格均值=30”。规格上限的标签设定同此步骤

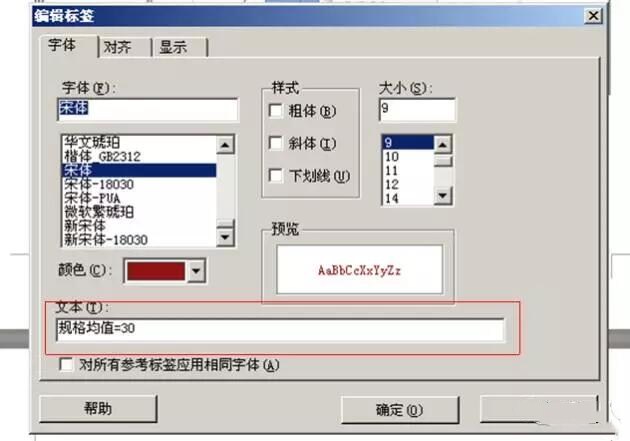
⑹ 以下便是完整的直方图：