英国威廉希尔体育公司-威廉希尔官方网站

英国威廉希尔体育公司在您身边

业务咨询：
marketing@infinityqs.cn

在线服务：
service@infinityqs.cn

电话：400-812-1268
010-65699909

使用正确的方法监控成批处理过程

当需要对化学溶液的质量特性进行监控时，有三种波动来源：随时间推移的平均值、批次内和批次之间。在这里我们以混合油漆为例阐述不同的统计方法。在油漆中，关键参数是固体的百分比，规格限是7.7  0.3。为了确定是否混合均匀，我们从每个批次中进行取样，每次从混合容器的不同的部位取样10次（表1）。我们先用最直接的但不正确的方式来分析数据。然后，我们用改良的方法来分析同样的数据，这种方法已经使用很多年，但目前很多程式化的SPC软件还不支持。

因为这种方法还没有很好为企业所了解，所以，目前依然处于“商业秘密”的阶段。然而对于英国威廉希尔体育公司SPC 软件，在例子中描述的方法已经全面支持。

图一: 混合容器

使用传统的控制图的不正确分析

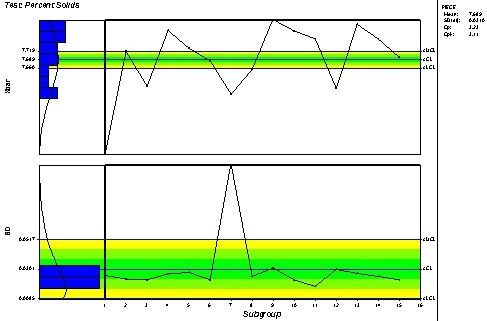
如果我们只用传统的控制图，我们会把每个批次的取样数10 作为子组样本大小来处理。这样的控制图看起来像是均值和标准差 (图2)。

图2: 不正确的分析。在上面的控制图中的控制限过窄，因为图中使用了批次内波动性替代了批次与批次之间的波动性。

此方法错误地在批次与批次图（均值图）的控制限计算上使用了批次内标准差（不是基于标准差图上的中心线）。这种常见错误会导致像图 2 这样的错误，控制限在均值图不能代表数据点。在这种情况下，控制限会非常窄，表示批次内波动性远远小于批次间的波动性。

使用 3D 控制图的正确分析

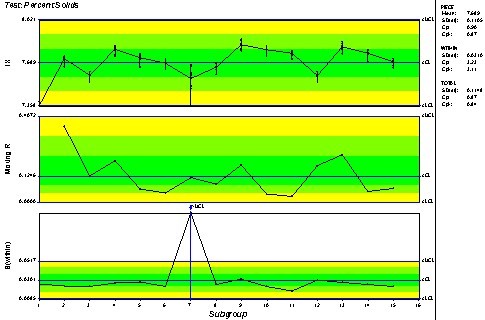
我们需要用两张图来跟踪波动性——移动极差图来跟踪批次和批次之间的波动性，标准差图（因为批次内子组大小是10）跟踪批次内波动性。现在用批次与批次间的移动极差图来计算批次与批次的均值图。图3显示了相同的数据，但是增加了移动极差图，在均值图上也显示了正确的控制限。（因为英国威廉希尔体育公司 SPC 处理数据，所以最上面的图现在是作为单值图来处理的单值）。

图3: 正确的分析——3D 控制图。移动极差图显示了了批次和批次间的波动性，S（批次内）图显示了批次内的波动性。上面的控制限是基于移动极差中心线。图的右侧统计批次与批次（件间），批次内（件内）和全部的波动性的组成。

在 IX 图上的突出点上的垂直线表示批次内的波动性。线的作用仅用于注释。注意批次内的批次#7的波动性性大于其它的批次。然而，此波动性仅限于批次内的，而不能作为在IX图或移动极差图波动的特殊原因来显示。

有很多时候，需要既监控子组内又需要监控子组之间的波动性。在这种情况下，3D 图正是此问题的解决方案。